Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
2.
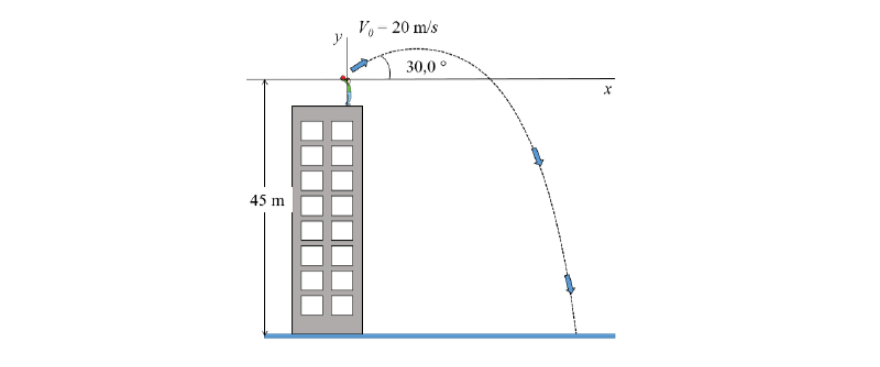
Se lanza una piedra hacia arriba desde la parte superior de un edificio en un ángulo de $30,0^{\circ}$ con la horizontal y con una velocidad inicial de 20,0 $\mathrm{m} / \mathrm{s}$. El punto de liberación está a $45,0 \mathrm{~m}$ respecto de la superficie de la Tierra. Considere despreciable la resistencia del aire.
b) Determine la velocidad de la piedra en el impacto.

b) Determine la velocidad de la piedra en el impacto.
Respuesta
Vamos con la siguiente...
Reportar problema
➡️ La velocidad de la piedra cuando impacta contra el piso
Para conocer la velocidad de la piedra en el impacto, necesitamos calcular las componentes $x$ e $y$ del vector velocidad justo en el instante en el cual toca el piso, que es el que encontramos en el ítem anterior, $t = 4.22 \, \text{s}$.
En este caso, $V_x$ es constante:
$V_x = 17.3 \, \frac{m}{s}$
Y evaluamos la ecuación de $V_y(t)$ en $t = 4.22 \, \text{s}$:
$V_y(4.22 \, \text{s}) = -31.356 \, \frac{m}{s}$
Perfecto, ya tenemos las componentes $x$ e $y$ del vector velocidad justo en el instante del impacto. Ahora, lo que nosotros estamos buscando es el módulo de ese vector (esa es la velocidad que tiene la piedra en ese instante)
$|\vec{V}| = \sqrt{V_x^2 + V_y^2}$
Reemplazando con lo que obtuvimos recién nos queda...
$|\vec{V}| = 35.8 \, \frac{m}{s}$
Por lo tanto, la velocidad de la piedra en el impacto es de $35.8 \, \frac{m}{s}$
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
